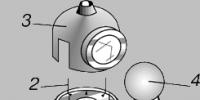
Ano ang konsepto ng matematika? Mga pamamaraan para sa pag-aaral ng mga konsepto ng matematika
Lektura 5. Mga konsepto sa matematika
1. Saklaw at nilalaman ng konsepto. Mga ugnayan sa pagitan ng mga konsepto
2. Kahulugan ng mga konsepto. Matukoy at hindi matukoy na mga konsepto.
3. Mga paraan ng pagtukoy ng mga konsepto.
4. Pangunahing konklusyon
Ang mga konsepto na itinuro sa isang panimulang kurso sa matematika ay karaniwang ipinakita sa apat na grupo. Ang una ay kinabibilangan ng mga konseptong nauugnay sa mga numero at operasyon sa mga ito: numero, karagdagan, termino, mas malaki, atbp. Ang pangalawa ay kinabibilangan ng mga konseptong algebraic: pagpapahayag, pagkakapantay-pantay, mga equation, atbp. Ang ikatlong pangkat ay binubuo ng mga geometric na konsepto: tuwid na linya, segment, tatsulok , atbp. .d. Ang ikaapat na pangkat ay binubuo ng mga konsepto na may kaugnayan sa mga dami at ang kanilang pagsukat.
Upang pag-aralan ang buong iba't ibang mga konsepto, kailangan mong magkaroon ng ideya ng konsepto bilang isang lohikal na kategorya at ang mga tampok ng mga konsepto sa matematika.
Sa lohika mga konsepto tiningnan bilang anyo ng pag-iisip, na sumasalamin sa mga bagay (mga paksa at phenomena) sa kanilang mga mahahalaga at pangkalahatang katangian. Ang linggwistikong anyo ng konsepto ay salita (term) o grupo ng mga salita.
Upang makabuo ng isang konsepto tungkol sa isang bagay ay nangangahulugan ng kakayahang makilala ito mula sa iba pang mga bagay na katulad nito. Ang mga konsepto ng matematika ay may ilang mga tampok. Ang pangunahing bagay ay mahalagang ang mga bagay sa matematika, kung saan napakahalaga na magbalangkas ng isang konsepto, ay hindi umiiral sa katotohanan. Ang mga bagay sa matematika ay nilikha ng isip ng tao. Ito ay mga perpektong bagay na sumasalamin sa mga tunay na bagay o phenomena. Halimbawa, sa geometry, pinag-aaralan nila ang hugis at sukat ng mga bagay nang hindi isinasaalang-alang ang iba pang mga katangian: kulay, masa, tigas, atbp. Abstract sila sa lahat ng ito. Para sa kadahilanang ito, sa geometry sa halip na ang salitang "object" sinasabi nila " geometric na pigura».
Ang resulta ng abstraction ay ang mga konseptong matematikal bilang "numero" at "magnitude".
Sa pangkalahatan, ang mga bagay sa matematika ay umiiral lamang sa pag-iisip ng tao at sa mga palatandaan at simbolo na nabubuo wikang matematikal.
Sa mga nasabi na, maaari nating idagdag iyon, ang pag-aaral spatial forms at quantitative relations ng materyal na mundo, ang matematika ay hindi lamang gumagamit ng iba't ibang mga diskarte sa abstraction, ngunit ang abstraction mismo ay gumaganap bilang isang multi-stage na proseso. Sa matematika, isinasaalang-alang nila hindi lamang ang mga konsepto na lumitaw sa panahon ng pag-aaral ng mga tunay na bagay, kundi pati na rin ang mga konsepto na lumitaw batay sa dating. Halimbawa, ang pangkalahatang konsepto ng isang function bilang isang sulat ay isang generalization ng mga konsepto ng mga partikular na function, ᴛ.ᴇ. isang abstraction mula sa abstractions.
- Saklaw at nilalaman ng konsepto. Mga ugnayan sa pagitan ng mga konsepto
Ang bawat bagay sa matematika ay may ilang mga katangian. Halimbawa, ang isang parisukat ay may apat na gilid, apat na tamang anggulo, at pantay na diagonal. Maaari mo ring tukuyin ang iba pang mga katangian nito.
Kabilang sa mga katangian ng isang bagay ay mayroong mahalaga at hindi gaanong mahalaga. Isinasaalang-alang ang ari-arian mahalaga para sa isang bagay kung ito ay likas sa bagay na ito at kung wala ito ay hindi ito umiiral. Halimbawa, para sa isang parisukat ang lahat ng mga katangian na nabanggit sa itaas ay mahalaga. Ang property na “side AB is horizontal” ay hindi mahalaga para sa isang square ABCD.
Kapag pinag-uusapan nila ang isang konsepto sa matematika, kadalasang nangangahulugan sila ng isang set ng mga bagay na tinutukoy ng isa termino(isang salita o grupo ng mga salita). Kaya, nagsasalita ng isang parisukat, ang ibig naming sabihin ay ang lahat ng mga geometric na numero na mga parisukat. Ito ay pinaniniwalaan na ang hanay ng lahat ng mga parisukat ay bumubuo sa saklaw ng konseptong "parisukat".
sa lahat, ang saklaw ng isang konsepto ay ang hanay ng lahat ng mga bagay na tinutukoy ng isang termino.
Ang anumang konsepto ay hindi lamang dami, kundi pati na rin ang nilalaman.
Isaalang-alang, halimbawa, ang konsepto ng "parihaba".
Ang saklaw ng konsepto ay isang hanay ng iba't ibang mga parihaba, at ang nilalaman nito ay kinabibilangan ng mga katangian ng mga parihaba bilang "may apat na tamang anggulo", "may pantay na magkabilang panig", "may pantay na mga diagonal", atbp.
Sa pagitan ng saklaw ng isang konsepto at nilalaman nito ay mayroong relasyon: kung tumaas ang dami ng isang konsepto, bababa ang nilalaman nito, at kabaliktaran. Kaya, halimbawa, ang saklaw ng konsepto na "parihaba" ay bahagi ng saklaw ng konsepto na "parihaba", at ang nilalaman ng konsepto na "parihaba" ay naglalaman ng higit pang mga katangian kaysa sa nilalaman ng konsepto na "parihaba" ("lahat ng panig ay pantay-pantay", "mga dayagonal ay magkaparehong patayo" at iba pa).
Ang anumang konsepto ay hindi matututunan nang hindi napagtatanto ang kaugnayan nito sa iba pang mga konsepto. Para sa kadahilanang ito, mahalagang malaman kung anong mga konsepto ng relasyon ang matatagpuan at upang maitatag ang mga koneksyon na ito.
Ang mga relasyon sa pagitan ng mga konsepto ay malapit na nauugnay sa mga relasyon sa pagitan ng kanilang mga volume, ᴛ.ᴇ. set.
Sumang-ayon tayo na tukuyin ang mga konsepto sa maliliit na titik ng alpabetong Latin: a, b, c, d, …, z.
Hayaang ibigay ang dalawang konsepto a at b. Tukuyin natin ang kanilang mga volume bilang A at B, ayon sa pagkakabanggit.
Kung A ⊂ B (A ≠ B), kung gayon sinasabi nila na ang konsepto a ay tiyak na may kaugnayan sa konsepto b, at ang konsepto b ay generic na may kaugnayan sa konsepto a.
Halimbawa, kung ang a ay isang "rectangle", ang b ay isang "quadrilateral", kung gayon ang kanilang mga volume A at B ay nasa inclusion relation (A ⊂ B at A ≠ B), at samakatuwid ang bawat rectangle ay isang quadrilateral. Para sa kadahilanang ito, maaari itong maitalo na ang konsepto ng "parihaba" ay tiyak na may kaugnayan sa konsepto ng "quadrangle", at ang konsepto ng "quadrangle" ay generic na may kaugnayan sa konsepto ng "parihaba".
Kung A = B, ang mga konseptong A at B ay sinasabing magkapareho.
Halimbawa, ang mga konsepto na "equilateral triangle" at "isosceles triangle" ay magkapareho, dahil ang kanilang mga volume ay nag-tutugma.
Isaalang-alang natin nang mas detalyado ang kaugnayan ng genus at species sa pagitan ng mga konsepto.
1. Una sa lahat, ang mga konsepto ng genus at species ay kamag-anak: ang parehong konsepto ay maaaring generic na may kaugnayan sa isang konsepto at tiyak na nauugnay sa isa pa. Halimbawa, ang konsepto ng "parihaba" ay generic na may kaugnayan sa konsepto ng "parisukat" at tiyak na may kaugnayan sa konsepto ng "quadrangle".
2. Pangalawa, para sa isang binigay na konsepto ay madalas na posibleng magpahiwatig ng ilang mga generic na konsepto. Kaya, para sa konsepto ng "rectangle" ang mga generic na konsepto ay "quadrangle", "parallelogram", "polygon". Sa mga ipinahiwatig, maaari mong ipahiwatig ang pinakamalapit. Para sa konsepto ng "rectangle" ang pinakamalapit na konsepto ay "parallelogram".
3. Pangatlo, nasa partikular na konsepto ang lahat ng katangian ng generic na konsepto. Halimbawa, ang isang parisukat, bilang isang tiyak na konsepto na may kaugnayan sa konsepto ng "parihaba", ay may lahat ng mga katangian na likas sa isang parihaba.
Dahil ang dami ng isang konsepto ay isang set, ito ay maginhawa, kapag nagtatatag ng mga relasyon sa pagitan ng mga volume ng mga konsepto, upang ilarawan ang mga ito gamit ang mga lupon ng Euler.
Itatag natin, halimbawa, ang ugnayan sa pagitan ng mga sumusunod na pares ng konsepto a at b kung:
1) a – “parihaba”, b – “rhombus”;
2) a – “polygon”, b – “paralelogram”;
3) a – “tuwid”, b – “segment”.
Ang mga ugnayan sa pagitan ng mga hanay ay ipinapakita sa figure, ayon sa pagkakabanggit
2. Kahulugan ng mga konsepto. Matukoy at hindi matukoy na mga konsepto.
Ang hitsura sa matematika ng mga bagong konsepto, at samakatuwid ay ang mga bagong termino na nagsasaad ng mga konseptong ito, ay nagpapahiwatig ng kanilang kahulugan.
Kahulugan karaniwang tinatawag na pangungusap na nagpapaliwanag sa kakanyahan ng isang bagong termino (o pagtatalaga). Bilang isang patakaran, ginagawa ito batay sa mga naunang ipinakilala na konsepto. Halimbawa, ang isang parihaba ay maaaring tukuyin tulad ng sumusunod: "Ang isang parihaba ay karaniwang tinatawag na isang quadrilateral na ang mga anggulo ay ayos." Ang kahulugan na ito ay may dalawang bahagi - ang tinukoy na konsepto (parihaba) at ang pagtukoy ng konsepto (isang quadrilateral na may lahat ng tamang anggulo). Kung tinutukoy natin ang unang konsepto sa pamamagitan ng a, at ang pangalawa sa pamamagitan ng b, kung gayon ang kahulugan na ito ay maaaring iharap sa sumusunod na anyo:
a ay (sa kahulugan) b.
Ang mga salitang "ay (sa kahulugan)" ay karaniwang pinapalitan ng simbolo ⇔, at pagkatapos ay ganito ang hitsura ng kahulugan:
Nabasa nila: "ang a ay katumbas ng b ayon sa kahulugan." Mababasa mo rin ang entry na ito sa ganitong paraan: “and if and only if b.
Ang mga depinisyon na may ganitong istraktura ay tinatawag halata naman. Tingnan natin ang mga ito nang mas malapitan.
Bumaling tayo sa ikalawang bahagi ng kahulugan ng "parihaba".
Kabilang dito ang:
1) ang konsepto ng "quadrangle", ĸᴏᴛᴏᴩᴏᴇ ay generic na may kaugnayan sa konsepto ng "rectangle".
2) ang ari-arian na "magkaroon ng lahat ng tamang anggulo", na nagpapahintulot sa amin na makilala ang isang uri mula sa lahat ng posibleng quadrilaterals - mga parihaba; sa bagay na ito, ito ay tinatawag na pagkakaiba ng species.
Sa pangkalahatan, ang mga partikular na pagkakaiba ay mga katangian (isa o higit pa) na ginagawang posible na makilala ang mga tinukoy na bagay mula sa saklaw ng generic na konsepto.
Ang mga resulta ng aming pagsusuri ay maaaring ipakita sa anyo ng isang diagram:

Ang "+" sign ay ginagamit upang palitan ang butil na "at".
Alam namin na ang anumang konsepto ay may dami. Kung ang konsepto a ay tinukoy sa pamamagitan ng genus at tiyak na pagkakaiba, kung gayon tungkol sa dami nito - ang set A - masasabi nating naglalaman ito ng mga bagay na kabilang sa set C (ang saklaw ng generic na konsepto c) at may ari-arian P:
A = (x/ x ∈ C at P(x)).
Dahil ang kahulugan ng isang konsepto sa pamamagitan ng genus at tiyak na pagkakaiba ay mahalagang isang kondisyon na kasunduan upang ipakilala ang isang bagong termino upang palitan ang anumang hanay ng mga kilalang termino, imposibleng sabihin ang tungkol sa kahulugan kung ito ay tama o mali; ito ay hindi napatunayan o hindi pinatutunayan. Ngunit kapag bumubuo ng mga kahulugan, sumusunod sila sa isang bilang ng mga patakaran. Pangalanan natin sila.
1. Ang kahulugan ay dapat proporsyonal. Nangangahulugan ito na ang saklaw ng tinukoy at pagtukoy ng mga konsepto ay dapat magkasabay.
2. Sa kahulugan (o kanilang sistema) hindi dapat magkaroon ng vicious circle. Nangangahulugan ito na ang isang konsepto ay hindi maaaring tukuyin sa mga tuntunin ng sarili nito.
3. Ang kahulugan ay dapat malinaw. Ito ay kinakailangan, halimbawa, na ang mga kahulugan ng mga terminong kasama sa pagtukoy ng konsepto ay malaman sa oras na ang kahulugan ng isang bagong konsepto ay ipinakilala.
4. Tukuyin ang parehong konsepto sa pamamagitan ng pagkakaiba ng genus at species, na sinusunod ang mga panuntunang binalangkas sa itaas, maaaring gawin sa iba't ibang paraan. Kaya, ang isang parisukat ay maaaring tukuyin bilang:
a) isang parihaba na ang mga katabing gilid ay pantay;
b) isang parihaba na ang mga dayagonal ay magkaparehong patayo;
c) isang rhombus na may tamang anggulo;
d) isang paralelogram kung saan ang lahat ng panig ay pantay at ang mga anggulo ay tama.
Ang iba't ibang mga kahulugan ng parehong konsepto ay posible dahil sa malaking bilang ng mga katangian na kasama sa nilalaman ng konsepto, iilan lamang ang kasama sa kahulugan. At pagkatapos ay ang isa ay pinili mula sa mga posibleng kahulugan, na nagpapatuloy kung saan ang isa ay mas simple at mas angkop para sa karagdagang pagbuo ng teorya.
Pangalanan natin ang pagkakasunud-sunod ng mga aksyon na dapat nating sundin kung gusto nating kopyahin ang kahulugan ng isang pamilyar na konsepto o bumuo ng isang kahulugan ng bago:
1. Pangalanan ang konsepto (term) na tinutukoy.
2. Ipahiwatig ang pinakamalapit na generic na konsepto (kaugnay ng tinukoy).
3. Ilista ang mga katangian na nakikilala ang mga tinukoy na bagay mula sa generic na volume, iyon ay, bumalangkas ng isang tiyak na pagkakaiba.
4. Suriin kung ang mga patakaran para sa pagtukoy ng konsepto ay natutugunan (ito ba ay proporsyonal, may mabisyo bang bilog, atbp.).
Lektura Blg. 2
matematika
Paksa: "Mga Konseptong Matematika"
Mga konsepto sa matematika
Kahulugan ng mga konsepto
Mga kinakailangan para sa pagtukoy ng mga konsepto
Ilang uri ng mga kahulugan
1. Mga konsepto sa matematika
Ang mga konsepto na pinag-aaralan sa isang paunang kurso sa matematika ay karaniwang ipinakita sa anyo ng apat na grupo. Ang una ay kinabibilangan ng mga konseptong nauugnay sa mga numero at mga operasyon sa mga ito: numero, karagdagan, termino, mas malaki, atbp. Ang pangalawa ay kinabibilangan ng mga konseptong algebraic: expression, pagkakapantay-pantay, equation, atbp. Ang pangatlo ay binubuo ng mga geometric na konsepto: tuwid na linya, segment, tatsulok, atbp. d. Ang ikaapat na pangkat ay binubuo ng mga konsepto na may kaugnayan sa mga dami at ang kanilang pagsukat.
Paano pag-aralan ang gayong kasaganaan ng iba't ibang mga konsepto?
Una sa lahat, kailangan mong magkaroon ng ideya ng konsepto bilang isang lohikal na kategorya at ang mga tampok ng mga konsepto ng matematika.
Sa lohika, ang mga konsepto ay itinuturing bilang isang anyo ng pag-iisip na sumasalamin sa mga bagay (mga bagay o phenomena) sa kanilang mga esensyal at pangkalahatang katangian. Ang linguistic form ng isang konsepto ay isang salita o grupo ng mga salita.
Upang makabuo ng isang konsepto tungkol sa isang bagay ay nangangahulugan ng kakayahang makilala ito mula sa iba pang mga bagay na katulad nito. Ang mga konsepto ng matematika ay may ilang mga tampok. Ang pangunahing bagay ay ang mga bagay sa matematika tungkol sa kung saan kinakailangan upang bumalangkas ng isang konsepto ay hindi umiiral sa katotohanan. Ang mga bagay sa matematika ay nilikha ng isip ng tao. Ito ay mga perpektong bagay na sumasalamin sa mga tunay na bagay o phenomena. Halimbawa, sa geometry ay pinag-aaralan nila ang hugis at sukat ng mga bagay nang hindi isinasaalang-alang ang iba pang mga katangian nila: kulay, masa, tigas, atbp. Sila ay ginulo mula sa lahat ng ito, abstract. Samakatuwid, sa geometry, sa halip na ang salitang "object" ay sinasabi nila ang "geometric figure".
Ang resulta ng abstraction ay ang mga konseptong matematikal bilang "numero" at "magnitude".
Sa pangkalahatan, ang mga bagay sa matematika ay umiiral lamang sa pag-iisip ng tao at sa mga palatandaan at simbolo na bumubuo ng wikang matematika.
Sa nasabi na, maaari nating idagdag na, kapag pinag-aaralan ang mga spatial form at quantitative na relasyon ng materyal na mundo, ang matematika ay hindi lamang gumagamit ng iba't ibang mga diskarte sa abstraction, ngunit ang abstraction mismo ay gumaganap bilang isang multi-stage na proseso. Sa matematika, isinasaalang-alang nila hindi lamang ang mga konsepto na lumitaw sa panahon ng pag-aaral ng mga tunay na bagay, kundi pati na rin ang mga konsepto na lumitaw batay sa dating. Halimbawa, ang pangkalahatang konsepto ng isang function bilang isang sulat ay isang generalization ng mga konsepto ng mga tiyak na function, i.e. isang abstraction mula sa abstractions.
Upang makabisado karaniwang mga diskarte Upang pag-aralan ang mga konsepto sa paunang kurso ng matematika, ang guro ay nangangailangan ng kaalaman tungkol sa saklaw at nilalaman ng konsepto, tungkol sa mga relasyon sa pagitan ng mga konsepto at tungkol sa mga uri ng mga kahulugan ng mga konsepto.
2. Saklaw at nilalaman ng konsepto. Mga ugnayan sa pagitan ng mga konsepto
Ang bawat bagay sa matematika ay may ilang mga katangian. Halimbawa, ang isang parisukat ay may apat na gilid, apat na tamang anggulo, at pantay na diagonal. Maaari mo ring tukuyin ang iba pang mga katangian nito.
Sa mga katangian ng isang bagay, nakikilala ang mahalaga at hindi mahalaga. Ang isang ari-arian ay itinuturing na mahalaga para sa isang bagay kung ito ay likas sa bagay na ito at kung wala ito ay hindi ito umiiral. Halimbawa, para sa isang parisukat ang lahat ng mga katangian na nabanggit sa itaas ay mahalaga. Ang pag-aari na "side AD ay pahalang" ay hindi mahalaga para sa isang parisukat na ABCD. Kung ang parisukat ay pinaikot, ang gilid AD ay matatagpuan sa ibang paraan (Larawan 26).
Samakatuwid, upang maunawaan kung ano ang isang ibinigay na bagay sa matematika, kailangan mong malaman ang mga mahahalagang katangian nito.
Kapag pinag-uusapan ng mga tao ang isang konseptong pangmatematika, kadalasang nangangahulugan sila ng isang set ng mga bagay na tinutukoy ng isang termino (isang salita o isang grupo ng mga salita). Kaya, nagsasalita ng isang parisukat, ang ibig naming sabihin ay ang lahat ng mga geometric na numero na mga parisukat. Ito ay pinaniniwalaan na ang hanay ng lahat ng mga parisukat ay bumubuo sa saklaw ng konseptong "parisukat".
Sa lahat ang saklaw ng isang konsepto ay ang hanay ng lahat ng mga bagay na tinutukoy ng isang termino.
Ang anumang konsepto ay hindi lamang dami, kundi pati na rin ang nilalaman.
Isaalang-alang, halimbawa, ang konsepto ng "parihaba".
Ang saklaw ng konsepto ay isang hanay ng iba't ibang mga parihaba, at ang nilalaman nito ay kinabibilangan ng mga katangian ng mga parihaba bilang "may apat na tamang anggulo", "may pantay na magkabilang panig", "may pantay na mga diagonal", atbp.
May kaugnayan sa pagitan ng dami ng isang konsepto at ng nilalaman nito: kung tumaas ang dami ng isang konsepto, bababa ang nilalaman nito, at kabaliktaran. Kaya, halimbawa, ang saklaw ng konsepto na "parihaba" ay bahagi ng saklaw ng konsepto na "parihaba", at ang nilalaman ng konsepto na "parihaba" ay naglalaman ng higit pang mga katangian kaysa sa nilalaman ng konsepto na "parihaba" ("lahat ng panig ay pantay-pantay", "mga dayagonal ay magkaparehong patayo", atbp.).
Ang anumang konsepto ay hindi maaaring matutunan nang hindi napagtatanto ang kaugnayan nito sa iba pang mga konsepto. Samakatuwid, mahalagang malaman kung anong mga konsepto ng relasyon ang matatagpuan at upang maitatag ang mga koneksyong ito.
Ang mga relasyon sa pagitan ng mga konsepto ay malapit na nauugnay sa mga relasyon sa pagitan ng kanilang mga volume, i.e. set.
Sumang-ayon tayo na tukuyin ang mga konsepto na may maliliit na titik ng alpabetong Latin: a, b, c,..., z.
Hayaang ibigay ang dalawang konsepto a at b. Tukuyin natin ang kanilang mga volume bilang A at B, ayon sa pagkakabanggit.
Kung ang  B (A ≠ B), pagkatapos ay sinasabi nila na ang konsepto a - tiyak na may kaugnayan sa konseptob, at ang konsepto b- generic kaugnay ng konsepto a.
B (A ≠ B), pagkatapos ay sinasabi nila na ang konsepto a - tiyak na may kaugnayan sa konseptob, at ang konsepto b- generic kaugnay ng konsepto a.
Halimbawa, kung ang a ay isang "parihaba", ang b ay isang "quadrangle", kung gayon ang kanilang mga volume na A at B ay nasa ugnayan ng pagsasama (A  B at A ≠ B), dahil ang bawat parihaba ay isang quadrilateral. Samakatuwid, maaari itong maitalo na ang konsepto ng "parihaba" ay tiyak na may kaugnayan sa konsepto ng "quadrangle", at ang konsepto ng "quadrangle" ay generic na may kaugnayan sa konsepto ng "parihaba".
B at A ≠ B), dahil ang bawat parihaba ay isang quadrilateral. Samakatuwid, maaari itong maitalo na ang konsepto ng "parihaba" ay tiyak na may kaugnayan sa konsepto ng "quadrangle", at ang konsepto ng "quadrangle" ay generic na may kaugnayan sa konsepto ng "parihaba".
Kung A = B, pagkatapos ay sinasabi nila iyon mga konsepto a atbay magkapareho.
Halimbawa, ang mga konsepto na "equilateral triangle" at "equiangular triangle" ay magkapareho, dahil ang kanilang mga volume ay nagtutugma.
Kung ang mga set A at B ay hindi nauugnay sa kaugnayan ng pagsasama, sasabihin nila na ang mga konsepto a at b ay wala sa kaugnayan ng genus at species at hindi magkapareho. Halimbawa, ang mga konseptong "tatsulok" at "parihaba" ay hindi konektado ng gayong mga ugnayan.
Isaalang-alang natin nang mas detalyado ang kaugnayan ng genus at species sa pagitan ng mga konsepto. Una, ang mga konsepto ng genus at species ay kamag-anak: ang parehong konsepto ay maaaring generic na may kaugnayan sa isang konsepto at tiyak na nauugnay sa isa pa. Halimbawa, ang konsepto ng "parihaba" ay generic na may kaugnayan sa konsepto ng "parisukat" at tiyak na may kaugnayan sa konsepto ng "quadrangle".
Pangalawa, para sa isang naibigay na konsepto ay kadalasang posible na tukuyin ang ilang mga generic na konsepto. Kaya, para sa konsepto ng "rectangle" ang mga generic na konsepto ay "quadrangle", "parallelogram", "polygon". Kabilang sa mga ito, maaari mong ipahiwatig ang pinakamalapit. Para sa konsepto ng "rectangle" ang pinakamalapit na konsepto ay "parallelogram".
Pangatlo, ang isang konsepto ng species ay may lahat ng mga katangian ng isang generic na konsepto. Halimbawa, ang isang parisukat, bilang isang tiyak na konsepto na may kaugnayan sa konsepto ng "parihaba", ay may lahat ng mga katangian na likas sa isang parihaba.
Dahil ang dami ng isang konsepto ay isang set, ito ay maginhawa, kapag nagtatatag ng mga relasyon sa pagitan ng mga volume ng mga konsepto, upang ilarawan ang mga ito gamit ang mga lupon ng Euler.
Itatag natin, halimbawa, ang ugnayan sa pagitan ng mga sumusunod na pares ng konsepto a at b kung:
1) a - "parihaba", b - "rhombus";
2) a - "polygon", b - "parallelogram";
3) a - "tuwid", b - "segment".
Sa kaso 1) ang mga volume ng mga konsepto ay nagsalubong, ngunit ni isang set ay isang subset ng isa pa (Larawan 27).

Dahil dito, maaari itong maitalo na ang mga konseptong ito a at b ay wala sa kaugnayan ng genus at species.
Sa kaso 2) ang mga volume ng ibinigay na mga konsepto ay nasa kaugnayan ng pagsasama, ngunit hindi nag-tutugma - bawat parallelogram ay isang polygon, ngunit hindi kabaligtaran (Fig. 28). Dahil dito, maaari itong maitalo na ang konsepto ng "parallelogram" ay tiyak na may kaugnayan sa konsepto ng "polygon", at ang konsepto ng "polygon" ay generic na may kaugnayan sa konsepto ng "parallelogram".

Sa kaso 3) ang mga volume ng mga konsepto ay hindi nagsalubong, dahil hindi isang solong segment ang masasabing isang tuwid na linya, at hindi isang solong tuwid na linya ang maaaring tawaging isang segment (Larawan 29).

Dahil dito, ang mga konseptong ito ay hindi nauugnay sa genus at species.
Tungkol sa mga konseptong "tuwid na linya" at "segment" ay masasabi nating sila ay may kaugnayan sa kabuuan at bahagi: Ang isang segment ay bahagi ng isang tuwid na linya, hindi ang uri nito. At kung ang isang konsepto ng species ay may lahat ng mga katangian ng isang generic na konsepto, kung gayon ang isang bahagi ay hindi kinakailangang magkaroon ng lahat ng mga katangian ng kabuuan. Halimbawa, ang isang segment ay walang kaparehong katangian ng isang tuwid na linya gaya ng infinity nito.
1.2. Mga uri at kahulugan ng mga konsepto ng matematika sa elementarya na matematika
Kapag naasimilasyon siyentipikong kaalaman Ang mga mag-aaral sa elementarya ay kinakaharap iba't ibang uri mga konsepto. Ang kawalan ng kakayahan ng mag-aaral na pag-iba-ibahin ang mga konsepto ay humahantong sa kanilang hindi sapat na asimilasyon.
Ang lohika sa mga konsepto ay nakikilala sa pagitan ng dami at nilalaman. Ang ibig sabihin ng volume ay ang klase ng mga bagay na nauugnay sa konseptong ito at pinagkakaisa nito. Kaya, ang saklaw ng konsepto ng tatsulok ay kinabibilangan ng buong hanay ng mga tatsulok, anuman ang kanilang mga tiyak na katangian (mga uri ng mga anggulo, laki ng mga gilid, atbp.).
Upang ipakita ang nilalaman ng isang konsepto, kinakailangan upang maitaguyod sa pamamagitan ng paghahambing kung anong mga tampok ang kinakailangan at sapat upang i-highlight ang kaugnayan nito sa iba pang mga bagay. Hanggang sa maitatag ang nilalaman at mga katangian, ang kakanyahan ng bagay na sinasalamin ng konseptong ito ay hindi malinaw, imposibleng tumpak at malinaw na makilala ang bagay na ito mula sa mga katabi nito, at ang pagkalito ng pag-iisip ay nangyayari.
Halimbawa, para sa konsepto ng isang tatsulok, ang mga naturang katangian ay kinabibilangan ng mga sumusunod: isang closed figure, na binubuo ng tatlong tuwid na mga segment. Ang hanay ng mga katangian kung saan ang mga bagay ay pinagsama sa isang klase ay tinatawag na kinakailangan at sapat na mga katangian. Sa ilang mga konsepto, ang mga tampok na ito ay umaakma sa isa't isa, na bumubuo sa nilalaman kung saan ang mga bagay ay pinagsama sa isang solong klase. Ang mga halimbawa ng naturang mga konsepto ay tatsulok, anggulo, bisector at marami pang iba.
Ang kabuuan ng mga bagay na ito na napapailalim sa konseptong ito, ay bumubuo ng isang lohikal na klase ng mga bagay.
Ang isang lohikal na klase ng mga bagay ay isang koleksyon ng mga bagay na may mga karaniwang katangian, bilang isang resulta kung saan ang mga ito ay ipinahayag ng isang karaniwang konsepto. Ang lohikal na klase ng mga bagay at ang saklaw ng kaukulang konsepto ay nag-tutugma.
Ang mga konsepto ay nahahati sa mga uri ayon sa nilalaman at saklaw, depende sa kalikasan at bilang ng mga bagay kung saan inilalapat ang mga ito.
Batay sa kanilang saklaw, ang mga konsepto ng matematika ay nahahati sa indibidwal at pangkalahatan. Kung ang saklaw ng isang konsepto ay kinabibilangan lamang ng isang bagay, ito ay tinatawag na solong.
Mga halimbawa ng mga solong konsepto: "ang pinakamaliit na dalawang-digit na numero", "ang numero 5", "isang parisukat na may haba ng gilid na 10 cm", "isang bilog na may radius na 5 cm".
Ang pangkalahatang konsepto ay sumasalamin sa mga katangian ng isang tiyak na hanay ng mga bagay. Ang dami ng naturang mga konsepto ay palaging mas malaki kaysa sa dami ng isang elemento.
Mga halimbawa pangkalahatang konsepto: “set ng dalawang-digit na numero”, “triangles”, “equation”, “hindi pagkakapantay-pantay”, “mga numerong multiple ng 5”, “mga aklat-aralin sa matematika para sa elementarya”.
Ang mga konsepto ay tinatawag na conjunctive kung ang kanilang mga tampok ay magkakaugnay at indibidwal na wala sa mga ito ang nagpapahintulot sa pagtukoy ng mga bagay ng klase na ito ay konektado sa pamamagitan ng conjunction na "at". Halimbawa, ang mga bagay na nauugnay sa konsepto ng isang tatsulok ay kinakailangang binubuo ng tatlong tuwid na mga segment at sarado.
Sa iba pang mga konsepto, ang ugnayan sa pagitan ng kinakailangan at sapat na mga katangian ay naiiba: hindi sila umakma sa bawat isa, ngunit pinapalitan ang bawat isa. Nangangahulugan ito na ang isang katangian ay katumbas ng isa pa. Ang isang halimbawa ng ganitong uri ng ugnayan sa pagitan ng mga katangian ay maaaring maging mga palatandaan ng pagkakapantay-pantay ng mga segment at anggulo. Ito ay kilala na ang klase ng pantay na mga segment ay kinabibilangan ng mga segment na: a) alinman nag-tutugma kapag superimposed; b) o hiwalay na katumbas ng pangatlo; c) o binubuo ng pantay na bahagi, atbp.
Sa kasong ito, ang mga nakalistang katangian ay hindi kinakailangan nang sabay-sabay, tulad ng kaso sa magkakaugnay na uri ng mga konsepto; dito, isang katangian lamang mula sa lahat ng nakalista ay sapat na: bawat isa sa kanila ay katumbas ng alinman sa iba. Dahil dito, ang mga palatandaan ay konektado sa pamamagitan ng conjunction na "o". Ang ganitong koneksyon ng mga tampok ay tinatawag na disjunction, at ang mga konsepto ay naaayon na tinatawag na disjunctive.
Mahalaga rin na isaalang-alang ang paghahati ng mga konsepto sa ganap at kamag-anak.
Pinagsasama-sama ng mga ganap na konsepto ang mga bagay sa mga klase ayon sa ilang mga katangian na nagpapakilala sa kakanyahan ng mga bagay na ito. Kaya, ang konsepto ng anggulo ay sumasalamin sa mga katangian na nagpapakilala sa kakanyahan ng anumang anggulo tulad nito. Ang sitwasyon ay katulad ng maraming iba pang mga geometric na konsepto: bilog, sinag, rhombus, atbp.
Pinagsasama-sama ng mga kamag-anak na konsepto ang mga bagay sa mga klase ayon sa mga katangian na nagpapakilala sa kanilang kaugnayan sa iba pang mga bagay. Kaya, ang konsepto ng mga patayong linya ay nakukuha kung ano ang nagpapakilala sa relasyon ng dalawang linya sa bawat isa: intersection, ang pagbuo ng isang tamang anggulo. Katulad nito, ang konsepto ng numero ay sumasalamin sa kaugnayan sa pagitan ng sinusukat na dami at ng tinatanggap na pamantayan.
Ang mga kamag-anak na konsepto ay nagdudulot ng mas malubhang kahirapan para sa mga mag-aaral kaysa sa mga ganap na konsepto. Ang kakanyahan ng mga paghihirap ay namamalagi sa katotohanan na ang mga mag-aaral ay hindi isinasaalang-alang ang relativity ng mga konsepto at nagpapatakbo sa kanila bilang ganap na mga konsepto. Kaya, kapag hiniling ng guro sa mga mag-aaral na gumuhit ng patayo, ang ilan sa kanila ay gumuhit ng patayo. Espesyal na atensyon dapat bigyang pansin ang konsepto ng numero.
Ang numero ay ang ratio ng kung ano ang binibilang (haba, timbang, dami, atbp.) sa pamantayan na ginagamit para sa pagtatasa na ito. Malinaw, ang bilang ay nakasalalay sa parehong dami na sinusukat at sa pamantayan. Kung mas malaki ang sinusukat na halaga, mas malaki ang numero na magkakaroon ng parehong pamantayan. Sa kabaligtaran, mas malaki ang pamantayan (sukat), mas maliit ang bilang kapag tinatantya ang parehong halaga. Dahil dito, dapat na maunawaan ng mga mag-aaral sa simula pa lang na ang mga paghahambing ng mga numero sa pamamagitan ng magnitude ay maaari lamang gawin kapag mayroon silang parehong pamantayan sa likod ng mga ito. Sa katunayan, kung, halimbawa, ang lima ay nakuha kapag sinusukat ang haba sa sentimetro, at tatlo ang nakuha kapag nagsusukat sa metro, kung gayon ang tatlo ay nagpapahiwatig ng mas malaking halaga kaysa sa lima. Kung hindi nauunawaan ng mga mag-aaral ang kamag-anak na katangian ng mga numero, mahihirapan silang matutunan ang sistema ng numero.
Ang mga kahirapan sa pag-master ng mga kamag-anak na konsepto ay nananatili sa mga mag-aaral sa gitna at maging sa mataas na paaralan.
Halimbawa, ang konseptong "parihaba" ay may mas maliit na saklaw kaysa sa saklaw ng konseptong "parihaba" dahil ang anumang parisukat ay isang parihaba, ngunit hindi bawat parihaba ay isang parisukat. Samakatuwid, ang konsepto ng "parisukat" ay may higit na nilalaman kaysa sa konsepto ng "parihaba": ang isang parisukat ay may lahat ng mga katangian ng isang parihaba at ilang iba pa (lahat ng panig ng isang parisukat ay pantay, ang mga diagonal ay magkaparehong patayo).
Sa proseso ng pag-iisip, ang bawat konsepto ay hindi umiiral nang hiwalay, ngunit pumapasok sa ilang mga koneksyon at relasyon sa iba pang mga konsepto. Sa matematika, isang mahalagang anyo ng koneksyon ang pag-asa na partikular sa genus.
Halimbawa, isaalang-alang ang mga konseptong "parihaba" at "parihaba". Ang saklaw ng konseptong "parisukat" ay bahagi ng saklaw ng konseptong "parihaba". Samakatuwid, ang una ay tinatawag na species, at ang pangalawa - generic. Sa mga ugnayan ng genus-species, dapat na makilala ng isa ang konsepto ng pinakamalapit na genus at ang mga sumusunod na generic na yugto.
Halimbawa, para sa uri na "parisukat" ang pinakamalapit na genus ay ang genus na "parihaba", para sa isang parihaba ang pinakamalapit na genus ay ang genus na "parallelogram", para sa isang "parallelogram" - "quadrilateral", para sa isang "quadrilateral" - "polygon", at para sa isang "polygon" - " flat figure."
Sa elementarya, sa unang pagkakataon, ang bawat konsepto ay ipinakilala nang biswal, sa pamamagitan ng pagmamasid sa mga partikular na bagay o praktikal na operasyon (halimbawa, kapag binibilang ang mga ito). Ang guro ay umaasa sa kaalaman at karanasan ng mga bata na kanilang nakuha edad preschool. Ang pagiging pamilyar sa mga konsepto ng matematika ay naayos gamit ang isang termino o isang termino at isang simbolo.
Ang pamamaraang ito ng pagtatrabaho sa mga konsepto ng matematika sa mababang Paaralan ay hindi nangangahulugan na ang kursong ito ay hindi gumagamit iba't ibang uri mga kahulugan.
Upang tukuyin ang isang konsepto ay ilista ang lahat ng mahahalagang katangian ng mga bagay na kasama sa konseptong ito. Ang pandiwang kahulugan ng isang konsepto ay tinatawag na termino.
Halimbawa, ang "numero", "tatsulok", "bilog", "equation" ay mga termino.
Ang kahulugan ay nalulutas ang dalawang problema: kinikilala at nakikilala nito ang isang tiyak na konsepto mula sa lahat ng iba at ipinapahiwatig ang mga pangunahing tampok na kung wala ang konsepto ay hindi maaaring umiral at kung saan nakasalalay ang lahat ng iba pang mga tampok.
Ang kahulugan ay maaaring higit pa o hindi gaanong malalim. Ito ay depende sa antas ng kaalaman tungkol sa konsepto na ibig sabihin. Kung mas kilala natin siya, mas malaki ang posibilidad na makapagbigay tayo para sa kanya pinakamahusay na kahulugan.
Sa pagsasagawa ng pagtuturo sa mga bata sa elementarya, ang tahasan at implicit na mga kahulugan ay ginagamit.
Ang mga tahasang kahulugan ay nasa anyo ng pagkakapantay-pantay o pagkakaisa ng dalawang konsepto.
Halimbawa: "Ang propedeutics ay isang panimula sa anumang agham." Narito ang dalawang konsepto ay tinutumbasan ng isa sa isa - "propaedeutics" at "pagpasok sa anumang agham."
Sa kahulugan na "Ang isang parisukat ay isang parihaba kung saan ang lahat ng panig ay pantay-pantay," mayroon kaming isang pagkakataon ng mga konsepto.
Sa pagtuturo sa mga bata sa elementarya, ang kontekstwal at ostensive na mga kahulugan ay partikular na interes sa mga implicit na kahulugan.
Anumang sipi mula sa teksto, maging anumang konteksto, kung saan nangyayari ang konsepto na kinagigiliwan natin, sa ilang pag-unawa, ang implicit na kahulugan nito. Ang konteksto ay naglalagay ng isang konsepto na may kaugnayan sa iba pang mga konsepto at sa gayon ay ipinapakita ang nilalaman nito.
Halimbawa, kapag nagtatrabaho sa mga bata, gamit ang mga expression tulad ng "hanapin ang kahulugan ng expression", "ihambing ang kahulugan ng mga expression na 5 + a at (a - 3) × 2, kung a = 7", "basahin ang mga expression na ay mga kabuuan", "basahin ang mga expression, at pagkatapos ay basahin ang mga equation," pinalawak namin ang konsepto ng "mathematical expression" bilang isang talaan na binubuo ng mga numero o variable at mga palatandaan ng pagkilos.
Halos lahat ng mga depinisyon na nakatagpo natin Araw-araw na buhay Ito ay mga kahulugan sa konteksto. Nang marinig ang isang hindi kilalang salita, sinisikap nating itatag ang kahulugan nito sa ating sarili batay sa lahat ng sinabi.
Ang isang katulad na bagay ay nangyayari sa pagtuturo sa mga batang mag-aaral. Maraming mga konsepto sa matematika sa elementarya ang binibigyang kahulugan sa pamamagitan ng konteksto. Ito ay, halimbawa, mga konsepto tulad ng "malaki - maliit", "anumang", "anuman", "isa", "marami", "numero", "pagpapatakbo ng aritmetika", "equation", "gawain", atbp. .d.
Ang mga kahulugan sa konteksto ay nananatiling hindi kumpleto at hindi kumpleto. Ginagamit ang mga ito dahil sa hindi kahandaan ng mga batang mag-aaral na makabisado ang buong, at lalo na pang-agham, kahulugan.
Ang mga ostensive na kahulugan ay mga kahulugan sa pamamagitan ng pagpapakita. Ang mga ito ay kahawig ng mga ordinaryong kahulugan sa konteksto, ngunit ang konteksto dito ay hindi isang sipi ng anumang teksto, ngunit ang sitwasyon kung saan ang bagay na itinalaga ng konsepto ay nahahanap ang sarili nito.
Halimbawa, ang guro ay nagpapakita ng isang parisukat (drawing o papel na modelo) at nagsasabing "Tingnan mo - ito ay isang parisukat." Ito ay isang tipikal na ostensive na kahulugan.
Sa elementarya, ginagamit ang mga ostensive na kahulugan kapag isinasaalang-alang ang mga konsepto tulad ng "pula (puti, itim, atbp.) na kulay", "kaliwa - kanan", "kaliwa pakanan", "digit", "nauuna at kasunod na numero", " signs” arithmetic operations”, "comparative signs", "triangle", "quadrangle", "cube", atbp.
Batay sa ostensive assimilation ng mga kahulugan ng mga salita, posibleng ipakilala ang pandiwang kahulugan ng mga bagong salita at parirala sa diksyunaryo ng bata. Ostensive na mga kahulugan - at sila lamang - nag-uugnay ng mga salita sa mga bagay. Kung wala ang mga ito, ang wika ay isang verbal lace lamang na walang layunin, substantive na nilalaman.
Tandaan na sa elementarya, ang mga katanggap-tanggap na kahulugan tulad ng "Gagamitin namin ang salitang "pentagon" upang nangangahulugang isang polygon na may limang panig." Ito ang tinatawag na "nominal definition".
Mayroong iba't ibang tahasang kahulugan na ginagamit sa matematika. Ang pinakakaraniwan sa mga ito ay ang pagpapasiya sa pamamagitan ng pinakamalapit na katangian ng genus at species. Ang pangkaraniwang kahulugan ay tinatawag ding klasikal.
Mga halimbawa ng mga kahulugan sa pamamagitan ng genus at mga partikular na katangian: "Ang parallelogram ay isang quadrilateral na ang magkabilang panig ay magkatulad", "Ang isang rhombus ay isang parallelogram na ang mga gilid ay pantay", "Ang isang parihaba ay isang parallelogram na ang mga anggulo ay tama", "Ang isang parisukat ay isang parihaba na ang mga gilid ay pantay", "Ang isang rhombus na may tamang mga anggulo ay tinatawag na isang parisukat."
Tingnan natin ang mga kahulugan ng isang parisukat. Sa unang kahulugan, ang pinakamalapit na genus ay magiging "parihaba," at ang partikular na tampok ay "lahat ng panig ay pantay." Sa pangalawang kahulugan, ang pinakamalapit na genus ay "rhombus", at ang tiyak na karakter ay "mga tamang anggulo".
Kung hindi natin kukunin ang pinakamalapit na genus ("parallelogram"), magkakaroon ng dalawang partikular na katangian ng isang parisukat: "Ang parisukat ay isang paralelogram kung saan ang lahat ng panig ay pantay at ang lahat ng mga anggulo ay tama."
Sa generic na kaugnayan mayroong mga konsepto ng "pagdaragdag (pagbabawas, pagpaparami, paghahati)" at "pagpapatakbo ng aritmetika", ang konsepto ng "talamak (kanan, mahina ang ulo) anggulo" at "anggulo".
Walang napakaraming halimbawa ng mga tahasang ugnayan ng genus-species sa maraming konseptong matematikal na tinatalakay sa mga pangunahing baitang. Ngunit isinasaalang-alang ang kahalagahan ng kahulugan sa pamamagitan ng genus at species sa karagdagang edukasyon, ipinapayong tiyakin na nauunawaan ng mga mag-aaral ang kakanyahan ng kahulugan ng species na ito na nasa elementarya na baitang.
Maaaring isaalang-alang ng magkakahiwalay na kahulugan ang isang konsepto ayon sa paraan ng pagbuo o paglitaw nito. Ang ganitong uri ng pagpapasiya ay tinatawag na genetic.
Mga halimbawa ng genetic na kahulugan: "Ang anggulo ay ang mga sinag na lumalabas mula sa isang punto," "Ang dayagonal ng isang parihaba ay isang segment na nag-uugnay sa magkasalungat na mga vertex ng isang parihaba." Sa elementarya, ginagamit ang mga genetic na kahulugan para sa mga konsepto gaya ng "segment", "broken line", "right angle", "circle".
Ang mga genetic na konsepto ay maaari ding tukuyin sa pamamagitan ng isang listahan.
Halimbawa, "Ang natural na serye ng mga numero ay ang mga numero 1, 2, 3, 4, atbp."
Ang ilang mga konsepto sa elementarya ay ipinakilala lamang sa pamamagitan ng termino.
Halimbawa, ang mga yunit ng oras ay taon, buwan, oras, minuto.
May mga konsepto sa elementarya na mga baitang na ipinakita sa simbolikong wika sa anyo ng pagkakapantay-pantay, halimbawa, a ×1= a, a× 0=0
Sa elementarya, maraming mga konseptong pangmatematika ang unang natutunan nang mababaw at malabo. Sa unang kakilala, ang mga mag-aaral ay natututo lamang tungkol sa ilang mga katangian ng mga konsepto at may isang napaka-makitid na ideya ng kanilang saklaw. At ito ay natural. Hindi lahat ng konsepto ay madaling maunawaan. Ngunit walang duda na ang pag-unawa at napapanahong paggamit ng guro sa ilang uri ng mga kahulugan ng mga konseptong matematikal ay isa sa mga kondisyon para sa mga mag-aaral na magkaroon ng matatag na kaalaman tungkol sa mga konseptong ito.
Kabilang sa mga kasanayang itinuturo ng matematika at kailangan ninyong matutunan ay: pinakamahalaga may kakayahan uriin mga konsepto.
Ang katotohanan ay ang matematika, tulad ng maraming iba pang mga agham, ay hindi nag-aaral ng mga indibidwal na bagay o phenomena, ngunit malaki at mabigat. Kaya, kapag nag-aaral ka ng mga tatsulok, pinag-aaralan mo ang mga katangian ng anumang mga tatsulok, at mayroong isang walang katapusang bilang ng mga ito. Sa pangkalahatan, ang saklaw ng anumang konsepto ng matematika ay, bilang panuntunan, walang hanggan.
Upang makilala ang mga bagay ng mga konsepto ng matematika at pag-aralan ang kanilang mga katangian, ang mga konseptong ito ay karaniwang nahahati sa mga uri at klase. Sa katunayan, bilang karagdagan sa mga pangkalahatang katangian, ang anumang konsepto ng matematika ay may mas maraming mahahalagang katangian na hindi likas sa lahat ng mga bagay ng konseptong ito, ngunit sa mga bagay lamang ng isang tiyak na uri. Kaya, ang mga tamang tatsulok, bilang karagdagan sa mga pangkalahatang katangian ng anumang mga tatsulok, ay may maraming mga katangian na napakahalaga para sa pagsasanay, halimbawa. Pythagorean theorem, ugnayan sa pagitan ng mga anggulo at panig, atbp.
Sa proseso ng mga siglo-lumang pag-aaral ng mga konsepto sa matematika, sa proseso ng kanilang maraming mga aplikasyon sa buhay, sa iba pang mga agham, ang ilang mga espesyal na uri ay nakilala mula sa kanilang saklaw, na may mga pinaka-kagiliw-giliw na mga katangian, na kung saan ay madalas na nakatagpo at ginagamit sa pagsasanay. . Kaya, mayroong isang walang katapusang bilang ng iba't ibang mga quadrilateral, ngunit sa pagsasagawa, sa teknolohiya, ang ilang mga uri lamang ng mga ito ang pinaka ginagamit: mga parisukat, parihaba, parallelogram, rhombus, trapezoid.
Ang paghahati sa saklaw ng isang tiyak na konsepto sa mga bahagi ay ang pag-uuri ng konseptong ito. Mas tiyak, ang pag-uuri ay nauunawaan bilang ang pamamahagi ng mga bagay ng isang konsepto sa magkakaugnay na mga klase (species, uri) ayon sa pinakamahalagang katangian (properties). Ang tanda (pag-aari) kung saan ginawa ang pag-uuri (dibisyon) ng isang konsepto sa mga uri (mga klase) ay tinatawag batayan mga klasipikasyon.
Ang isang wastong itinayong pag-uuri ng isang konsepto ay sumasalamin sa mga pinakamahalagang katangian at koneksyon sa pagitan ng mga bagay ng konsepto, tumutulong upang mas mahusay na mag-navigate sa hanay ng mga bagay na ito, at ginagawang posible na maitatag ang mga katangian ng mga bagay na ito na pinakamahalaga para sa aplikasyon ng ang konseptong ito sa iba pang mga agham at pang-araw-araw na kasanayan.
Ang pag-uuri ng isang konsepto ay ginawa ayon sa isa o higit pa sa mga pinakamahalagang batayan.
Kaya, ang mga tatsulok ay maaaring uriin ayon sa laki ng kanilang mga anggulo. Nakukuha namin ang mga sumusunod na uri: acute-angled (lahat ng anggulo ay acute), rectangular (isang anggulo ay tuwid, ang iba ay acute), obtuse-angled (isang anggulo ay obtuse, ang iba ay acute). Kung kukunin natin ang mga ugnayan sa pagitan ng mga panig bilang batayan para sa paghahati ng mga tatsulok, pagkatapos ay makukuha natin ang mga sumusunod na uri: scalene, isosceles at regular (equilateral).
Ito ay mas mahirap kapag kailangan mong uriin ang isang konsepto sa ilang mga batayan. Kaya, kung ang convex quadrilaterals ay inuri ayon sa parallelism ng kanilang mga gilid, kung gayon mahalagang kailangan nating hatiin ang lahat ng convex quadrilaterals nang sabay-sabay ayon sa dalawang pamantayan: 1) isang pares ng magkasalungat na panig ay parallel o hindi; 2) ang pangalawang pares ng magkasalungat na panig ay kahanay o hindi. Bilang resulta, nakakakuha tayo ng tatlong uri ng convex quadrilaterals: 1) quadrilaterals na may hindi magkatulad na panig; 2) quadrilaterals na may isang pares ng parallel na panig - trapezoids; 3) quadrilaterals na may dalawang pares ng parallel na gilid ay parallelograms.
Kadalasan, ang isang konsepto ay inuri sa mga yugto: una ayon sa isang batayan, pagkatapos ang ilang mga uri ay nahahati sa mga subspecies ayon sa isa pang batayan, atbp. Ang isang halimbawa ay ang pag-uuri ng mga quadrangles. Sa unang yugto, nahahati sila batay sa convexity. Pagkatapos ay ang convex quadrilaterals ay nahahati batay sa parallelism ng magkabilang panig. Sa turn, ang mga paralelogram ay nahahati batay sa pagkakaroon ng mga tamang anggulo, atbp.
Kapag nagsasagawa ng pag-uuri, dapat sundin ang ilang mga patakaran. Ipahiwatig natin ang mga pangunahing.
- Bilang batayan para sa pag-uuri, ang isa ay maaari lamang kumuha ng isang karaniwang katangian ng lahat ng mga bagay ng isang ibinigay na konsepto. Kaya, halimbawa, imposibleng kunin bilang batayan para sa pag-uuri ng mga algebraic na expression ang tanda ng pag-aayos ng mga termino sa mga kapangyarihan ng ilang variable. Ang tampok na ito ay hindi karaniwan sa lahat ng algebraic na expression, halimbawa, hindi ito makatuwiran para sa mga fractional na expression o monomial. Ang mga polynomial lang ang may ganitong feature, kaya ang mga polynomial ay maaaring uriin ayon sa pinakamataas na antas ng pangunahing variable.
- Ang batayan para sa pag-uuri ay dapat na ang mga mahahalagang katangian (mga tampok) ng mga konsepto. Isaalang-alang natin muli ang konsepto ng isang algebraic expression. Isa sa mga katangian ng konseptong ito ay ang mga variable na kasama sa isang algebraic expression ay itinalaga ng ilang mga titik. Ang pag-aari na ito ay pangkalahatan, ngunit hindi mahalaga, dahil ang likas na katangian ng expression ay hindi nakasalalay sa kung anong titik ang isang partikular na variable ay tinutukoy. Kaya, algebraic expression x+y At a+b- ito ay mahalagang parehong expression. Samakatuwid, hindi mo dapat pag-uri-uriin ang mga expression batay sa pagtatalaga ng mga variable sa pamamagitan ng mga titik. Ito ay isa pang bagay kung, bilang batayan para sa pag-uuri ng mga algebraic na expression, kinukuha namin ang tanda ng uri ng mga aksyon kung saan ang mga variable ay konektado, iyon ay, ang mga aksyon na ginagawa sa mga variable. Ang pangkalahatang tampok na ito ay napakahalaga, at ang pag-uuri ayon sa tampok na ito ay magiging tama at kapaki-pakinabang.
- Sa bawat yugto ng pag-uuri, isang batayan lamang ang maaaring gamitin. Imposibleng sabay-sabay na uriin ang isang konsepto ayon sa dalawang magkaibang pamantayan. Halimbawa, imposibleng pag-uri-uriin ang mga tatsulok nang sabay-sabay pareho sa laki at sa ugnayan sa pagitan ng mga gilid, dahil bilang isang resulta makakakuha tayo ng mga klase ng mga tatsulok na may mga karaniwang elemento (halimbawa, acute at isosceles o obtuse at isosceles, atbp. ). Ang sumusunod na kinakailangan sa pag-uuri ay nilabag dito: Bilang resulta ng pag-uuri sa bawat yugto, ang mga resultang klase (mga uri) ay hindi dapat magsalubong.
- Sa parehong oras Ang pag-uuri sa anumang batayan ay dapat na kumpleto at ang bawat bagay ng konsepto ay dapat mahulog sa isa at isang klase lamang bilang resulta ng pag-uuri.
Samakatuwid, ang paghahati ng lahat ng integer sa positibo at negatibo ay hindi tama, dahil ang integer zero ay hindi nahuhulog sa alinman sa mga klase. Dapat itong sabihin sa ganitong paraan: ang mga integer ay nahahati sa tatlong klase - positibo, negatibo at ang numerong zero.
Kadalasan, kapag nag-uuri ng mga konsepto, ilang mga klase lamang ang malinaw na nakikilala, habang ang iba ay ipinahiwatig lamang. Kaya, halimbawa, kapag nag-aaral ng mga algebraic na expression, kadalasan ang mga ganitong uri ng mga expression ay nakikilala: monomials, polynomials, fractional expression, hindi makatwiran. Ngunit ang mga uri na ito ay hindi nauubos ang lahat ng mga uri ng algebraic expression, kaya ang pag-uuri na ito ay hindi kumpleto.
Ang isang kumpletong tamang pag-uuri ng mga algebraic na expression ay maaaring gawin bilang mga sumusunod.
Sa unang yugto ng pag-uuri ng mga algebraic expression, nahahati sila sa dalawang klase: rational at irrational. Sa ikalawang yugto, ang mga rational expression ay nahahati sa mga integer at fraction. Sa ikatlong yugto, ang mga integer na expression ay nahahati sa monomials, polynomials at complex integer expression.
Ang pag-uuri na ito ay maaaring ilarawan bilang mga sumusunod
Gawain 7
7.1. Bakit hindi maaaring uriin ang mga rational na numero ayon sa kanilang pagkakapare-pareho?
7.2. Tukuyin kung tama ang paghahati ng konsepto:
a) Ang mga halaga ay maaaring pantay o hindi pantay.
b) Ang mga function ay maaaring tumaas o bumaba.
c) Ang mga isosceles triangle ay maaaring talamak, kanan o mahina.
d) Ang mga parihaba ay mga parisukat at rhombus.
7.3. Hatiin ang konsepto ng "geometric figure" ayon sa pag-aari ng pag-okupa ng bahagi ng isang eroplano at magbigay ng mga halimbawa ng bawat uri.
7.4. Bumuo ng mga posibleng scheme ng pag-uuri para sa mga rational na numero.
7.5. Bumuo ng scheme ng pag-uuri para sa mga sumusunod na konsepto:
a) quadrangle;
b) dalawang anggulo.
7.6. Uriin ang mga sumusunod na konsepto:
a) tatsulok at bilog;
b) mga anggulo sa isang bilog;
c) dalawang bilog;
d) tuwid na linya at bilog;
e) mga parisukat na equation;
f) isang sistema ng dalawang first-degree na equation na may dalawang hindi alam.
Ang mga ostensive na kahulugan ay mga kahulugan na nagpapakilala ng isang konsepto sa pamamagitan ng pagpapakita, na nagpapakita ng mga bagay na itinalaga ng terminong ito.
Ang matematika, hindi tulad ng ibang mga agham, ay nag-aaral sa mundo sa paligid natin mula sa isang espesyal na pananaw. Ang anumang mga bagay na pangmatematika ay resulta ng paghihiwalay ng quantitative at spatial na katangian at mga relasyon mula sa mga bagay at phenomena. yun. hindi talaga umiiral ang mga bagay sa matematika. Ang mga ito ay mga ideyal na konsepto; umiiral lamang ang mga ito sa mga kaisipan ng tao at sa mga palatandaan at simbolo na bumubuo ng wikang matematika. Bukod dito, sa pagbuo ng mga konsepto sa matematika, bilang karagdagan sa abstraction, kinikilala sila ng mga katangian na walang tunay na bagay na nagtataglay.
Pangunahing konsepto ng matematika: punto, linya, eroplano, numero, numero, magnitude, operasyon ng aritmetika.
Ang anumang konsepto ng matematika ay nailalarawan sa pamamagitan ng isang termino, dami at nilalaman.
Ang termino ay isang salita o grupo ng mga salita na nagpapangalan sa mga elemento ng isang tiyak na hanay. Ang saklaw ng isang konsepto ay ang bilang ng lahat ng mga bagay na tinutukoy ng parehong termino. Mayroong mahahalagang at hindi mahahalagang katangian ng mga bagay. Ang isang ari-arian ay magiging mahalaga kung ito ay likas sa isang bagay, at kung wala ito ang bagay ay hindi maaaring umiral. Non-essential - ang kawalan nito ay hindi nakakaapekto sa mahahalagang bagay.
a-ang konsepto ng paralelogram; c-konsepto ng parihaba; √vs√a isang generic para sa; c-species para sa isang; c-konsepto ng quadrilateral. √а с√с
Ang parehong konsepto, halimbawa, isang paralelogram, ay maaaring generic para sa konsepto ng isang parihaba o partikular para sa konsepto ng isang may apat na gilid.
Mga konsepto ng isosceles triangle. At isang hugis-parihaba na tatsulok. Wala sila sa mga relasyon sa genus-species. May mga ugnayan sa pagitan ng mga konsepto ng bahagi at kabuuan.
Halimbawa, ang isang sinag ay bahagi ng isang tuwid na linya, ang isang segment ay isang bahagi ng isang tuwid na linya, ang isang arko ay isang bahagi ng isang bilog.
Kung ang mga konsepto ay nasa mga ugnayang partikular sa genus, ang sumusunod na koneksyon ay umiiral sa pagitan ng dami ng konsepto at ng nilalaman nito: mas malaki ang volume, mas mababa ang nilalaman nito at kabaliktaran.
Ang kahulugan ng mga konsepto ay lohikal na operasyon, inilalantad ang nilalaman ng konsepto. Ipinapahiwatig nito ang mga mahahalagang katangian na sapat para sa pagkilala nito. Ang mga kahulugan ay nahahati sa tahasan at implicit (di-tuwiran). Ang mga tahasang kahulugan ay nasa anyo ng pagkakapantay-pantay, ang pagkakatulad ng dalawang konsepto.
Halimbawa: Ang paralelogram ay tinatawag. isang may apat na gilid na ang mga gilid ay magkaparehong magkatulad. at mayroong sa; a-parallelogram (pagtukoy sa konsepto; b-quadrilateral, ang mga gilid nito ay pairwise parallel (pagtukoy sa konsepto; a=r+v
Tinukoy na konsepto = generic na konsepto + tiyak na pagkakaiba
Genus-specific: Angle bisector ay tinatawag. isang sinag na umuusbong mula sa tuktok ng isang anggulo at hinahati ang anggulo sa kalahati / r-generic na konsepto: ray; konsepto ng v-species: umuusbong mula sa vertex ng isang anggulo at hinahati ang anggulo sa kalahati. Sa elementarya, bihirang ginagamit ang tahasang kahulugan sa pamamagitan ng pagkakaiba ng genus at species. Halimbawa: Kahulugan ng even number, rectangle, square, multiplication.
Ang mga tahasang kahulugan ay maaaring magkaroon ng isa pang istraktura: a) mga genetic na kahulugan. Ang isang tatsulok ay isang figure na binubuo ng 3 puntos na hindi nakahiga sa parehong linya, at 3 mga segment na nagkokonekta sa kanila sa pagkakasunud-sunod Isang generic na konsepto at paraan ng pagbuo.
b) paulit-ulit (recursion-return) Ang aritmetika na pag-unlad ay isang numerical sequence, ang bawat miyembro nito, simula sa pangalawa, ay katumbas ng nauna, idinagdag sa pare-parehong numero d para sa isang naibigay na sequence (pagkakaiba).
Sa elementarya, nangingibabaw ang mga implicit na kahulugan. Ang mga implicit na kahulugan ay maaaring kontekstwal o ostensive. Mga kahulugan sa konteksto - sa mga kahulugang ito, ang nilalaman ng mga bagong konsepto ay inihayag sa pamamagitan ng konteksto, pagsusuri ng isang tiyak na sitwasyon na naglalarawan sa kahulugan ng ipinakilalang konsepto. Halimbawa: 2+x=5
2. Ang mga mag-aaral sa elementarya ay inaalok ang mga sumusunod na gawain:
1) Aling figure ang kakaiba? Ipaliwanag ang iyong sagot.